nmr_sims.spin_system¶

This module provides the SpinSystem class, allowing specification of a specific spin system according to the nuclear idenitites, isotropic chemical shifts, and J-couplings of each spin, along with the temperature and magnetic field they are subjected to.

The SpinSystem class is used by all experiment simulation functions to derive the equilibrium operator and Hamiltonians required.

class nmr_sims.spin_system.SpinSystem(spins, default_nucleus='1H', field='500MHz', temperature='298K')[source]¶

Object representing a particular spin system.

This represents an ensemble of many identical spin systems subject to a specified temperature and magnetic field strength.

Create an instance SpinSystem.

Parameters

spins (Dict[int, Dict]) –
A dictionary with information on each spin that makes up the system. Below is an example of a valid format. This specifies a three proton (AMX) system, with the following parameters:

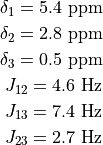
$\delta_1 = 5.4\ \mathrm{ppm} \delta_2 = 2.8\ \mathrm{ppm} \delta_3 = 0.5\ \mathrm{ppm} J_{12} = 4.6\ \mathrm{Hz} J_{13} = 7.4\ \mathrm{Hz} J_{23} = 2.7\ \mathrm{Hz}$
```
spins = {
    1: {
        "shift": 5.4,
        "couplings": {
            2: 4.6,
            3: 7.4,
        },
    },
    2: {
        "shift": 2.8,
        "couplings": {
            3: 2.7,
        },
    },
    3: {
        "shift": 0.5,
    },
}
```
Note that there is no need to repeat coupling information. As the coupling between spins 1 and 2 has been specified within the entry for spin 1, there is no need to repeat this for spin 2. Similary, spin 3 has been given no explicit coupling information as this has already been provided in the specification of spins 1 and 2.

Each entry in the spins dictionary should have an int as a key and a dict as its value. Within the each dict, the following key-value pairs are permitted:
- "shift" (necessary) - The isotropic chemical shift of the spin in ppm.
- "couplings" (optional) - The scalar couplings between the spin and its coupling partners. This should be denoted by a dict with an int key specifying the coupling partner, and a float value, specifying the J-coupling in Hz.
- "nucleus" (optional) - The identity of nucelus giving rise to the spin. If not specified, then default_nucleus will be used. Can be either an instance of nmr_sims.nuclei.Nucleus of a string corresponding to one of the pre-defined nuclei.
default_nucleus (Union[Nucleus, str]) – The nucleus identity of any spin in the spins dictionary that is not given an explicit "nucleus" key. By default, all unspecified nuclei will correspond to proton (¹H).
field (Union[int, float, str]) –
The magnetic field strength. The following inputs are valid:
- A positive number (int or float). The field will be taken to be in Telsa.
- A str satisfying the regex r"\d+T". Again, the field will be taken to be in Tesla
- A str satisfying the regex r"\d+MHz". This corresponds to the field which induces the specified Larmor frequency for proton.
By default, this is set as "500MHz", correponding to approximately 11.74T.
temperature (Union[int, float, str]) –
The temperature. The following inputs are valid:
- A positive number (int or float). The field will be taken to be in Kelvin.
- A str satisfying the regex r"\d+K". Again, the field will be taken to be in Kelvin.
- A str satisfying the regex r"-?\d+C". The temperature will be taken to be in Celcius.
warning:: (..) –
Current bug

Negative Celcius specifications ("-\d+C") are not supported currently, and will raise an error if given. PLease manually convert to Kelvin.

Ix(nucleus=None)[source]¶

Return the 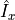$\hat{I}_x$ operator correpsonding to the system, with the option of specifying the nucelus to target.

For a given nucleus 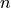$n$ , this is given by: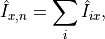

$\hat{I}_{x, n} = \sum_{i} \hat{I}_{ix},$

$\forall i \in \{1, \cdots, N\}$ satisfying the requirement that spin 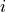$i$ corresponds to nucelus $n$ .

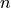Parameters: nucleus (Optional[str]) – The identity of the nucelus to target. If None, no constraint will be put on the nucleus.
Return type: Operator

Iy(nucleus=None)[source]¶

Return the $\hat{I}_y$ operator correpsonding to the system, with the option of specifying the nucelus to target.

For a given nucleus 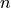$n$ , this is given by: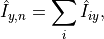

$\hat{I}_{y, n} = \sum_{i} \hat{I}_{iy},$

$\forall i \in \{1, \cdots, N\}$ satisfying the requirement that spin 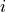$i$ corresponds to nucelus $n$ .

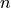Parameters: nucleus (Optional[str]) – The identity of the nucelus to target. If None, no constraint will be put on the nucleus.
Return type: Operator

Iz(nucleus=None)[source]¶

Return the 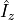$\hat{I}_z$ operator correpsonding to the system, with the option of specifying the nucelus to target.

For a given nucleus 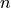$n$ , this is given by: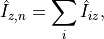

$\hat{I}_{z, n} = \sum_{i} \hat{I}_{iz},$

$\forall i \in \{1, \cdots, N\}$ satisfying the requirement that spin 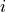$i$ corresponds to nucelus $n$ .

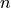Parameters: nucleus (Optional[str]) – The identity of the nucelus to target. If None, no constraint will be put on the nucleus.
Return type: Operator

property basic_frequencies: numpy.ndarray¶

Return the baisc (laboratory frame) frequencies of each spin.

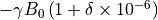
Given by $-\gamma B_0 \left(1 + \delta \times 10^{-6}\right)$

Return type: ndarray

property boltzmann_factor: Iterable[float]¶

Return the Boltzmann factor for each spin in the spin system.

This factor is given by 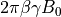$2 \pi \beta \gamma B_0$ . See inverse_temperature() for the definition of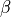 $\beta$ .

Return type: Iterable[float]

property equilibrium_operator: nmr_sims._operators.Operator¶

Return the equilibrium operator of the spin system.

Given by:

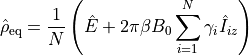
$\hat{\rho}_{\mathrm{eq}} = \frac{1}{N} \left(\hat{E} + 2 \pi \beta B_0 \sum_{i=1}^N \gamma_i \hat{I}_{iz}\right)$

Where 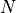$N$ is the number of spins, and 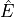$\hat{E}$ is the identity operator.

Return type: Operator

exclude_couplings()[source]¶

Spin system’s couplings will be turned off.

Can be reversed with include_couplings().

Return type: None

hamiltonian(offsets=None, decouple=None)[source]¶

Return the Hamiltonian for the spin system.

Given by:

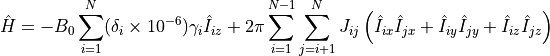
$\hat{H} = -B_0 \sum_{i=1}^N (\delta_i \times 10^{-6}) \gamma_i \hat{I}_{iz} + 2 \pi \sum_{i=1}^{N-1} \sum_{j=i+1}^N J_{ij} \left( \hat{I}_{ix} \hat{I}_{jx} + \hat{I}_{iy} \hat{I}_{jy} + \hat{I}_{iz} \hat{I}_{jz} \right)$

Parameters: offsets (Optional[dict]) – Specification of transmitter offsets for given nuclei, in units of Hz. As an example, the argument {"1H": 5000} would inorporate a transmtter offset of 5000Hz for proton.
Return type: Operator

include_couplings()[source]¶

Spin system’s couplings will be turned on.

Can be reversed with exclude_couplings().

Return type: None

property inverse_temperature: float¶

Return the inverse temperature for the system.

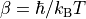Given by $\beta = \hbar / k_{\mathrm{B}} T$ .

Return type: float

classmethod new_random(nspins=3, ncouplings=None, max_couplings=3, shifts_range=(0.0, 10.0), couplings_range=(3.0, 15.0), field='500MHz', temperature='298K')[source]¶

Create a new instance with random chemical shifts and offsets.

Note

Only homonucler ¹H spin systems are available currently.

Parameters

nspins (Union[int, Tuple[int, int]]) – The number of spins the system should comprise.
ncouplings (Optional[int]) – The total number of couplings featured in the spin system. This must be a value satisfying ncouplings <= int(0.5 * (nspins * (nspins - 1))) There is a possibility that the final spin system will have fewer couplings than those stated if the random network of couplings does not satisfy the constraint placed by max_couplings.
max_couplings (Optional[int]) – The largest possible number of coupling interactions any particular spin may have.
shifts_range (Tuple[float, float]) – The smallest and greatest values of chemical shift any particular spin may have.
couplings_range (Tuple[float, float]) – The smallest and greatest values of scalar coupling any particular interaction may have.
field (Union[int, float, str]) – See __init__()
temperature (Union[int, float, str]) – See __init__()

Return type

SpinSystem

pulse(nucleus, phase=0.0, angle=1.5707963267948966)[source]¶

Return the operator for a pulse targeting a specific nucleus, with specified phase and flip angle.

Parameters

nucleus (str) – The identity of the nucleus to be targeted. Should match the nucleus.name.
phase (float) – Desired phase of the pulse in radians.
Angle – Desired flip angle in radians.

Return type

Operator

property rotframe_frequencies: numpy.ndarray¶

Return the rotating frame frequencies for each spin.

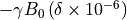
Given by $-\gamma B_0 \left(\delta \times 10^{-6}\right)$

Return type: ndarray

nmr_sims.spin_system¶

Related Topics

This Page